In this this video we are going to show the proof of one more fundamental identity of algebraIt states that (abc)²=a²b²c²2(abbcca)To derive thisIf `abc=9` and `abbcca=26`, find the value of `a^2b^2c^2`b2 =(a−b)22ab 3 (a b c)2 = a2 b2 c2 2(ab bc ca) 4 (a b) 3= a3 b3 3ab(a b);
Q Tbn And9gctffsuwllegbodlmoc6dmyqyir Djzm7vwtzshzjmf5m3wkeyz1 Usqp Cau
(ab+bc+ca)^2 formula
(ab+bc+ca)^2 formula-= a 2 ab ac ba b 2 bc ca cb c 2 Adding like terms, the final formula (worth remembering) is (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ac Practice Exercise for Algebra Module on Expansion of (a b c)The area of the ΔABC can be calculated using Heron's formula S = (AB BC AC)/2 = (10 17 21)/2 = 24 cm = √ 24(24 10) (24 17) (24 21) = 84 cm2 Step 5 Similarly, the area of the ΔACD can be calculated using Heron's formula S = (AC CD AD)/2 = (21 13 )/2 = 27 cm



What Is The Formula For A B C 2 Quora
Given that, a 2 b 2 c 2 = 50 and a b c = 12 We need to find ab bc ca Substitute the values of (a 2 b 2 c 2 ) and ( a b c ) in the identity (1), we have (12) 2 = 50 2 ( ab bc ca ) ⇒ 144 = 50 2 ( ab bc ca ) ⇒ 94 = 2 ( ab bc ca) ⇒ ab bc ca = `94/2` ⇒ ab bc caSocratic =>v=2ab2ca2bc =>2ab2ca=v2bc =>2a(bc)=v2bc =>a=(v2bc)/((2(bc)) Algebra Given v= 2(ab bc ca), how do you solve for a?
Section Formula With Examples Type I On finding the section point when the section ratio is given Example 1 Find the coordinates of the point which divides the line segment joining the points (6, 3) and (– 4, 5) in the ratio 3 2 internally Sol Let P (x, y) be the required pointb2 =(ab)2−2ab 2 (a−b)2 = a 2−2ab b; Get the list of basic algebra formulas in Maths at BYJU'S Stay tuned with BYJU'S to get all the important formulas in various chapters like trigonometry, probability and so on
SolutionShow Solution a 2 b 2 c 2 = 50 and ab bc ca = 47 Since ( a b c ) 2 = a 2 b 2 c 2 2 ( ab bc ca ) ∴ ( a b c ) 2 = 50 2 (47) ⇒ ( a b c ) 2 = 50 94 = 144 ⇒ a b c = `sqrt144 = 12` ∴ a b c = `12` Concept Expansion of Formula1 (a b)2 = a2 2ab b2;Click here👆to get an answer to your question ️ If a^2 b^2 c^2 ab bc ca = 0 , prove that a = b = c




A B C Is Equal To 9 And A B Ca Is Equal To 26 Maths Polynomials Meritnation Com




B2 C2 Ab Ca Formula Love Meme
The area of whole square is ( a b c) 2 geometrically The whole square is split as three squares and six rectangles So, the area of whole square is equal to the sum of the areas of three squares and six rectangles ( a b c) 2 = a 2 a b c a a b b 2 b c c a b c c 2 Now, simplify the expansion of the a b c wholeA 2 b 2 c 2 2ab 2bc 2ca = 625 a 2 b 2 c 2 2 (ab bc ca) = 625 a 2 b 2 c 2 2 × 59 = 625 Given, ab bc ca = 59 a 2 b 2 c 2 118 = 625 a 2 b 2 c 2 118 – 118 = 625 – 118 subtracting 118 from both the sides Therefore, a 2 b 2 c 2 = 507If a = 1001, b = 1002, c = 1003 , then value of a2 b2 c2 – ab – bc – ca isIn this video, we will understand short trick of Algebraic expressions a^2




A B C 0 Then Prove That A B C Ab Ca 2 Ab Ca Mathematics Topperlearning Com Eylmzlvv



Q Tbn And9gctffsuwllegbodlmoc6dmyqyir Djzm7vwtzshzjmf5m3wkeyz1 Usqp Cau
A plus b minus c Whole Square Formula To get formula / expansion for (a b c) 2, let us consider the formula / expansion for (a b c) 2 The formula or expansion for (a b c) 2 is (a b c) 2 = a 2 b 2 c 2 2ab 2bc 2ac In (a b c) 2, if c is negative, then we have (a b c) 2 In the terms of the expansion for (a b c) 2, consider the terms in which we find "c"You can check the formulas of A plus B plus C Whole cube in three ways We are going to share the (abc)^3 algebra formulas for you as well as how to create (abc)^3 and proof we can write we know that what is the formula of need too write in simple form of multiplication Simplify the all Multiplication one by oneUsing the 1/b 1/c = 2 and abc = 3 Solution To find a 2 b 2 c 2 Given that



Q Tbn And9gctojufww1jhxm1rgu39lejbc439efs4zaawb2xjxrsbx Hf2yjq Usqp Cau




ユニークab Ca 子供のための最高のぬりえ
The actual formula is (abc)² = a² b² c² 2 (ab bc ca) You can get this simple formula by multiplying (ab c) with (abc) (ab c)² = (ab c)* (ab c)Summary (abc)^2 If you have any issues in the (abc)^2 formulas, please let me know through social media and mail A Plus B Plus C Whole Square isClick here👆to get an answer to your question ️ Write the following in the expanded form (ab bc ca)^2



Www Imo Official Org Problems Imo08sl Pdf




If A B C 5 And Ab Ca 10 Then Prove That A3 C3 3abc 25 Mathematics Topperlearning Com T5wmjn
Consider, a2 b2 c2 – ab – bc – ca = 0 Multiply both sides with 2, we get 2 (a2 b2 c2 – ab – bc – ca) = 0 ⇒ 2a2 2b2 2c2 – 2ab – 2bc – 2ca = 0 2 Answers2 Active Oldest Votes 2 If a, b, and c are required to only be positive integers and some of them is 1, then we have a unique solution ( a, b, c) = ( 1, 1, 1) For solutions with a, b, c > 1, note that ( a − 1) ( b − 1) ( c − 1) = a b c − b c − c a − a b a b c − 1 = a b c − 3 Set x = a − 1, y = b −(abbcca)^2 formulaThe Health Gateway is a Ministry of Health initiative which provides BC residents and their families with secure access to a single view of their health information View and download your health information, such as COVID19 tests, COVID19 immunizations, medications, immunizations and health visitsEx 42, 7 By using properties of determinants, show that 8(−a2&ab




ユニークab Ca 子供のための最高のぬりえ
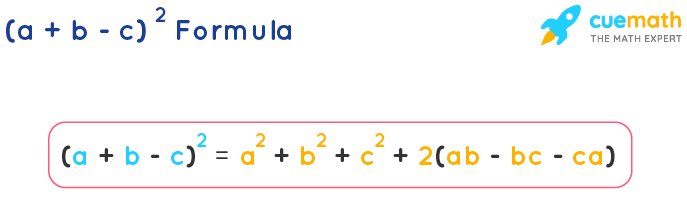



A Plus B Minus C Whole Square Formula A B C 2 Formula
Subhikshasampath (abc) 2 =a 2 b 2 c 2 2ab2bc2ca a 2 b 2 c 2 = (abc) 2 2ab2bc2ca a 2 b 2 c 2 = (7) 2 2 (abbcca) a 2 b 2 c 2 = (7) 2 2 () a 2 b 2 c 2 = 4940 a2b2c2= 9 There are various student are search formula of (ab)^3 and a^3b^3 Now I am going to explain everything below You can check and revert back if you like you can also check cube formula in algebra formula sheet a2 – b2 = (a – b)(a b) (ab)2 = a2 2ab b2 a2 b2 = (a –For more Questions Subscribe our Channel https//youtubecom/c/GRAVITYCOACHINGCENTRE?sub_confirmation=1




Quadratic Equation Session1 Ppt Video Online Download
.png)



Prove That A 2 B 2 C 2 Ab Ca Is Always Non Negative For All Values Of A Maths Polynomials Meritnation Com
Ab, V bc, and V ca (or phase voltages) into two symmetrical componentsV p andV n (of the line or phase voltages) The two balanced components are given by V VaV aV p = ab bc ca ⋅ ⋅2 3 (4) V VaV aV n = ab bc ca ⋅ ⋅2 3 (5) where aa=∠ ° =∠ °1 1 1 240and 2 The positive and negative sequence voltages can be used when ana Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeTriangular prism Volume and surface area of Triangular prism A prism with the triangle as the base is called triangular prism In the case of a triangular prism, two congruent and parallel triangles ABC and EFG are called the base of the prism




If A B C Is Equal To 12 And A Square B Square C Square Is Equal To 64 Find The Value Of Ab Brainly In




Curved Line In Formulas Tex Latex Stack Exchange
Click here👆to get an answer to your question ️ If a b c = 9 and ab bc ca = 26 , then find a^2 b^2 c^2Given that, a 2 b 2 c 2 = 35 and ab bc ca = 23 We need to find a b c Substitute the values of ( a 2 b 2 c 2 ) and ( ab bc ca ) in the identity (1), we have ( a b c ) 2 = 35 2 (23) ⇒ ( a b c ) 2 = 81 ⇒ a b c = `sqrt81` ⇒ a b c = `9` Concept Expansion of FormulaA3 −b3 =(a−b)33ab(a−b) 6 a2 −b2 =(ab)(a−b) 7 a3 −b3 =(a−b)(a2 ab b2) 8 a3 b3 =(ab)(a2 −ab b2) 9 a n−bn=(a−b)(an−1 a −2b an−3b2




Q17 A B 3 B C 3 C A 3 A A B C A 2 B 2 C 2 Ab Ca B A B B C C A
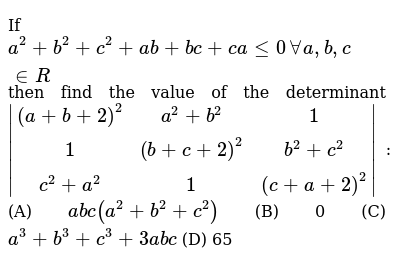



If A 2 B 2 C 2 Ab Ca 0 A B C In R Then Find The Value Of The Determinant A B 2 2 A 2 B 2 1 1 B C 2 2 B 2 C 2 C 2 A 2 1 C A 2 2 A Abc A 2 B 2 C 2
X³ (abc) x² (abbcca) xabc a² b² c² a b b c c a = ½ (ab)²(bc)²(ca)² (abc) (a² b² c² a bb cc a) = a³ b³ c³ 3 a b c Logarithms Math Formulas Product rule log ₐ (m n) = log ₐ m log ₐ nA² b² c² = (a b c)² 2 (ab bc ca)Wwwsakshieducationcom wwwsakshieducationcom 2 22 cos 2 ab c c ab − = ∴ 2bc 22 2 2 bc a bc − 2ac 22 2 2 ac b ac − 2ab 222 2 abc ab 22bc − a 2 a2 −cb22 a2 b2 − c = abc22 2 8 Prove that 222 22 2



What Is The Formula For A B C Quora



If B2 C2 Ab Ca 0 Prove That A B C Polynomials Maths Class 9
(a b c) 2 = a 2 b 2 c 2 2 (a b b c c a) The LHS of the above identity is a perfect square, hence it is always positive or 0 As stated in the title, I'm supposed to show that $(abc)^3 = a^3 b^3 c^3 (abc)(abacbc)$ My reasoning $$(a b c)^3 = (a b) c^3 = (a b)^3 3(a b)^2c 3(a b)c^2 c^3 Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share theirA3 b3 =(ab)−3ab(a b) 5 (a−b)3 = a3 −b3 −3ab(a−b);




Triangle Abc Ab 2x 2 3x 2 Ac X




0以上 Ab Ca Formula シモネタ
Where k is any integer (since net coefficients are integers) Now ((a2 b2 c2) k (ab bc ca) ) (abc) = a3b3c3−3abc The value of can be easily found out to be 1 (even by simply multiplying and comparing);Hence the other factor, (a2 b2 c2 ab bc ca) 41K answers 2M people helped The Formula is given below (a b c)³ = a³ b³ c³ 3 (a b) (b c) (a c) Explanation Let us just start with (abc)² = a² b² c²2ab2bc2ca =a² b² c²2 (abbcca) now



Find The Area Of Triangle Abc If Ab 3 4 And Gauthmath



Prove That B2 C2 Ab Ac Is Always Non Negative Polynomials Maths Class 9
Answer The required formula is Stepbystep explanation We are given to find the formula for the following expression We know that if x, y and z are any three real numbers, then the following identity holds Therefore, we get Thus, the required formula is taffy927x2 and 191 more users found this answer helpful heart outlined(ABBCCA)^2 =(ABBCCA)(ABBCCA) =(AB)^2AB^2CA^2BCAB^2C(BC)^2ABC^2A^2BCABC^2(CA)^2 =(AB)^2(BC)^2(CA)^22A^2BC2AB^2C2ABC^2 =(AB)^2(BC)^2(CA)^22(A^2BCAB^2CABC^2) =(AB)^2(BC)^2(CA)^22ABC(ABC) (or)Click here👆to get an answer to your question ️ If a b c = 9 and ab bc ca = 23 , then a^2 b^2 c^2 is equal to Join / Login maths If a b c = 9 and a b b c c a = 2 3, then a 2 b 2 c 2 is equal to A 3 5 B 5 8 C 1 2 7 D None of these Answer Correct option is A 3 5 Formula, (a b c) 2 = a 2 b 2 c 2




A B C 0 A 2 B 2 C 2 2 Ab Ac Youtube




If A B C 9 And Ab Ca 26 Find A B C Brainly In
Evaluate ( B2 C2 Ab Ca)(A B C) CISCE ICSE Class 7 Textbook Solutions 7008 Question Bank Solutions 6480 Concept Notes & Videos 150 Syllabus Advertisement Remove all ads Evaluate ( B2 C2 Ab Ca)(A B C) Mathematics Hence we have the other factor = (a2 b2 c2) k (ab bc ca) ;Recall the formula ` (abc)^2 = a^2 b^2 c^2 2 (ab bc ca)` Given that `a^2 b^2 c^2 = 250 , ab bc ca = 3 ` Then we have ` (abc)^2 = a^2 b^2 c^2 2 (ab bcca)` ` (abc)^2 = 250 2 (3)` ` (abc)^2 = 256` ` (abc) =± 16`




Find The Value Of A 3 B 3 C 3 3abc If 1 A B C 8 Ab Ca 19 2 A B C 5 A 2 B 2 C 2 1 Youtube




If A 2 B 2 C 2 1 Then What S The Range Of Ab Ac Quora
Using this formula (abc)² = a² b² c² 2 (ab bc ca)If a^2b^2c^2abbcca=0 then prove that a=b=c Get the answer to this question along with unlimited Maths questions and prepare better for JEE exam




What Will Be A B C If A B C 1 And Ab Ca 1 3 Quora




A B 3 B C 3 C A 3 A A B C A 2 B 2 C 2 Ab Ac B 3 A B B C C A C Youtube




If A B C 5 And Ab Ca 10 Prove A 3 B 3 C 3 3abc 25 Cbse Class 9 Maths Learn Cbse Forum




If B C 2 C A 2 A B 2 Are In Ap Prove That 1 B C 1 C A Youtube



In A Triangle Abc Median Ad Be And Cf Intersect At Point G Prove That 4 Ad Be Cf 3 Ab Ca Sarthaks Econnect Largest Online Education Community




Important Mathematical Formulas




If A 2 B 2 C 2 125 And Ab Ca 50 Find The Value Of A B C Brainly In
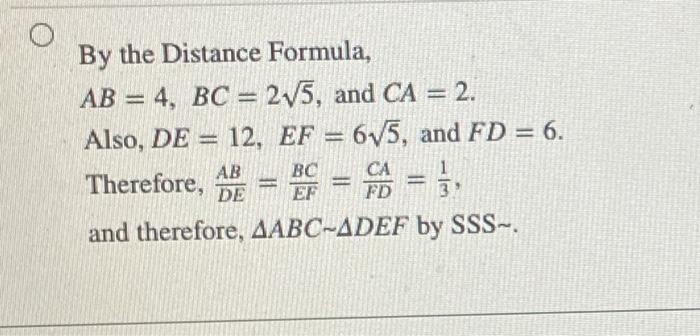



Solved Given Points A 0 0 B 4 0 C 0 2 D 0 0 E Chegg Com




If A B C Is Equals To 6 And A B Ca Is Equals To 11 Find A Cube Plus B Cube Plus C Cube Brainly In




Q3 Add The Following I Ab B Lido




Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf




Misc 4 Show That Either A B C 0 Or A B C Miscellaneous




B2 C2 Ab Ca Formula Love Meme
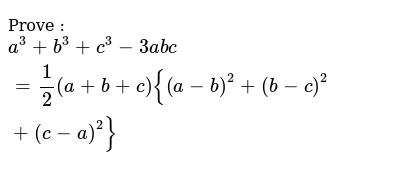



Prove A 3 B 3 C 3 3abc 1 2 A B C A B 2 B C 2 C A 2



How To Prove Ab Ac Cot B 2 For Any Triangle Quora




Prove A 3 B 3 C 3 3abc 1 2 A B C A B 2 B C 2 C A 2




Proving Of A B C 2 B2 C2 2 Ab Ca Cbse Board Ncert Mathematics In Hindi Youtube




Prove That The Determinant Is A B B C C A A 2 B 2 C 2 Mathematics Stack Exchange




If A B C 0 Then Prove That B C 2 3bc C A 2 3ca A B 2 3ab 1 Mathematics Topperlearning Com Sq6lgh



Boolean Expressions 1 Digital Design Analog Design Turnkey Asic Soc Embedded Firmware




Prove That The Determinant Is A B B C C A A 2 B 2 C 2 Mathematics Stack Exchange



7 If b2c226 Find The Value See How To Solve It At Qanda



How To Prove Math A 2 B 2 C 2 Ab Ca Math Is Non Negative For All Values Of Math A B Math And Math C Quora



How Do You Factor A B C Ab Ca Abc Socratic



What Is The Formula Of A B C 2 Quora




The Sides Ab And Ac Of A Triangle Abc Touch A Circle With Centre O And Radius R At P Q A Youtube




If The Roots Of The Equation A B X 2 B C X C A 0 Then Prove That B C 2a




If The Roots Of The Equation A B C X 2 B C A X C A B 0 Are Equal Then Show That 2 B 1 A 1 C Youtube
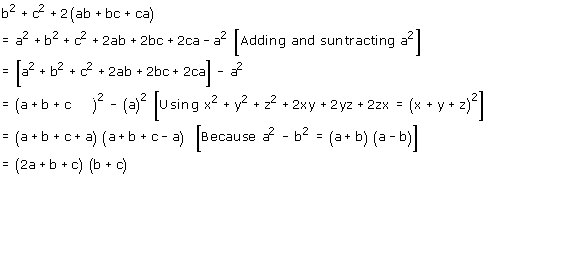



Factorise B2 C2 2 Ab Ca Mathematics Topperlearning Com Ollyvwb33



What Is The Formula For A B C Quora



コレクション 2ab Ca Formula シモネタ




If A 2 B 2 C 2 250 And Ab Ca 3 Then Find A B C




Algebraic Formulas
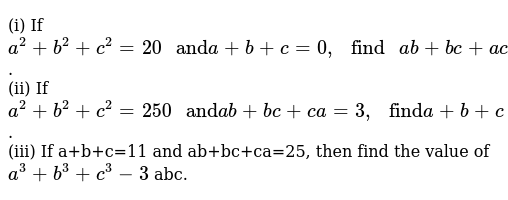



I If A 2 B 2 C 2 And A B C 0 Find Ab Ac Ii If A 2 B 2 C 2 250 And Ab Ca 3 Find A B C Iii If A B C 11 And Ab Ca 25 Then Find The Value Of A 3 B 3 C 3 3 Abc



If A B C 5 And Ab Ca 10 Then Prove That A3 C3 3abc 25 Studyrankersonline




Your Favorite Algebraic Maths Notes Formulas Facebook




2 2 Product Formulas Real Numbers A B C Whole Chegg Com




I Found K A B B C C A But What Is The Chegg Com



In Triangle Abc If D Is Any Point On Side Show That Ab Ca 2ad Quora




How To Prove Math A 2 B 2 C 2 Ab Ca Math Is Non Negative For All Values Of Math A B Math And Math C Quora



If The Mid Points Of The Sides Ab Ca Of A Triangle Are 1 5 1 0 4 2 2 3 4 Respectively Then The Length Of The Median From C To Ab Is What Quora



If A B C 7 And Ab Ca Find The Value Of A 2 B 2 C 2 Polynomials Maths Class 9




A B C 12 And B2 C2 50 Find Ab Ca Brainly In




0以上 Ab Ca Formula シモネタ
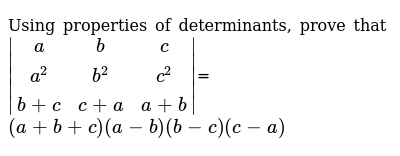



Using Properties Of Determinants Prove That A B C A 2 B 2 C 2 B C C A A B A B C A B B C C A




If A3 C3 3abc 1 2 A B C A B 2 B C 2 C A 2 Brainly In



1




If A B C 0 Then Show That B C B2 C A C2 A B 3abc 0 Novocom Top




B2 C2 Ab Ca Formula Love Meme




Factorise B2 2 Ab Ac Brainly In




Prove That A 2 B 2 C 2 Ab Ca Is Always Non Negative For All Valuesof A B And C Brainly In



What Is The Formula For A B C 2 Quora



What Is The Formula For A B C Quora




Algebraic Identities For Ssc Cgle Online Preparation Platform




Solved Given Points A 0 0 B 4 0 C 0 2 D 0 0 E Chegg Com




Q3 Add The Following I Ab B Lido




A Square Plus B Square Plus C Square Formula Examples A 2 B 2 C 2 Formula




If A 2 B 2 C 2 1 Then Ab Ca Lies In The Interval Youtube




Misc 4 Show That Either A B C 0 Or A B C Miscellaneous




In Abc Ab Ac 4 Then Its Length Of Altitude Is




If A B C 2 Ab Ca 1 And Abc 1 And Abc 2 Find The Value Of A 3 B 3 C 3




Misc 13 Using Determinants 3 A B C Ab Ac




Prove That The Determinant Is A B B C C A A 2 B 2 C 2 Mathematics Stack Exchange
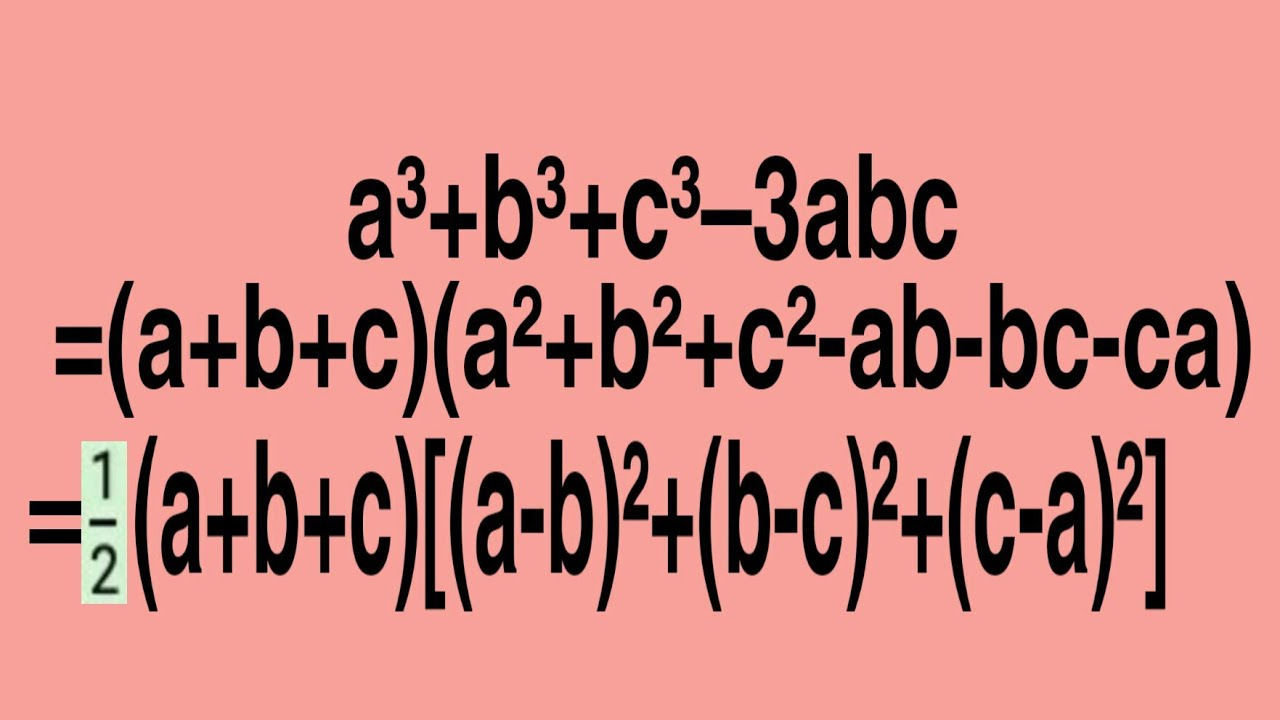



A B C 3abc A B C A B C Ab Ca 1 2 A B C A B B C C A Youtube



1




The Value Of A 3 B 3 C 3 3abc Ab Ca A 2 B 2 C 2 Is Where A 5 B 6 C 10




Chapter 2 Problem 15 15 15 Pts For Each Of The Following Functions F Ab Ac G A B A C Answersbay
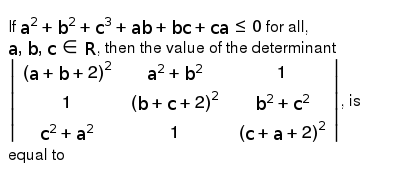



If A 2 B 2 C 3 Ab Ca Le 0 For All A B




If A B C 9 And Ab Ca 26 Find B2 C2 Brainly In




What Will Be A B C If A B C 1 And Ab Ca 1 3 Quora




If B C B C C A C A A B A B Are In Ap Then Show That 1 B C 1 C A 1 A B Are In Ap Use Add Ab Ca A 2 B 2 C 2 To Each Term Mathematics Topperlearning Com M2cbrr



If The Roots Of A B C X 2 B C A X C A B 0 Are Equal Then 1 A 1 B 1 C Youtube




If Quadratic Equation Ax 2 Bx Ab Ca A 2 B 2 C 2 0 Youtube




What S The Formula Of A B Quora Learning Math Math Math Equations



The Value Of Determinant A B B C A B C C A B C A A B C Is Studyrankersonline




Solved Given Points A 0 0 B 4 0 C 0 2 D 0 0 E Chegg Com



ユニークab Ca 子供のための最高のぬりえ




Alpha Beta Maths Formula Quadratic Equation Math Formulas



0 件のコメント:
コメントを投稿