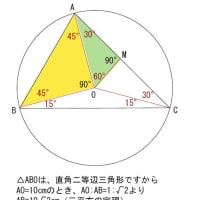
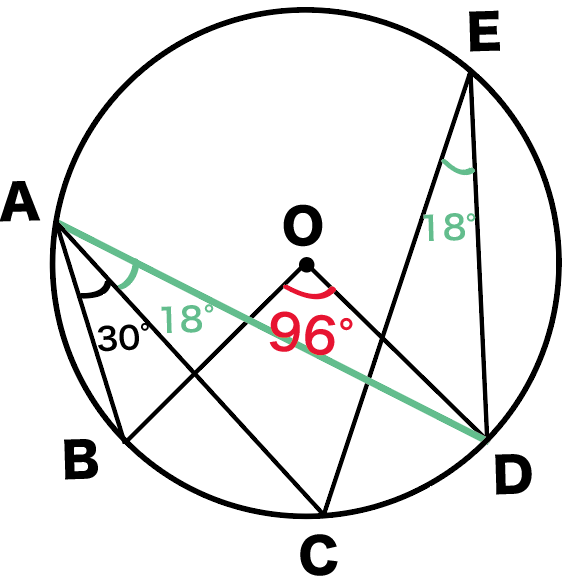
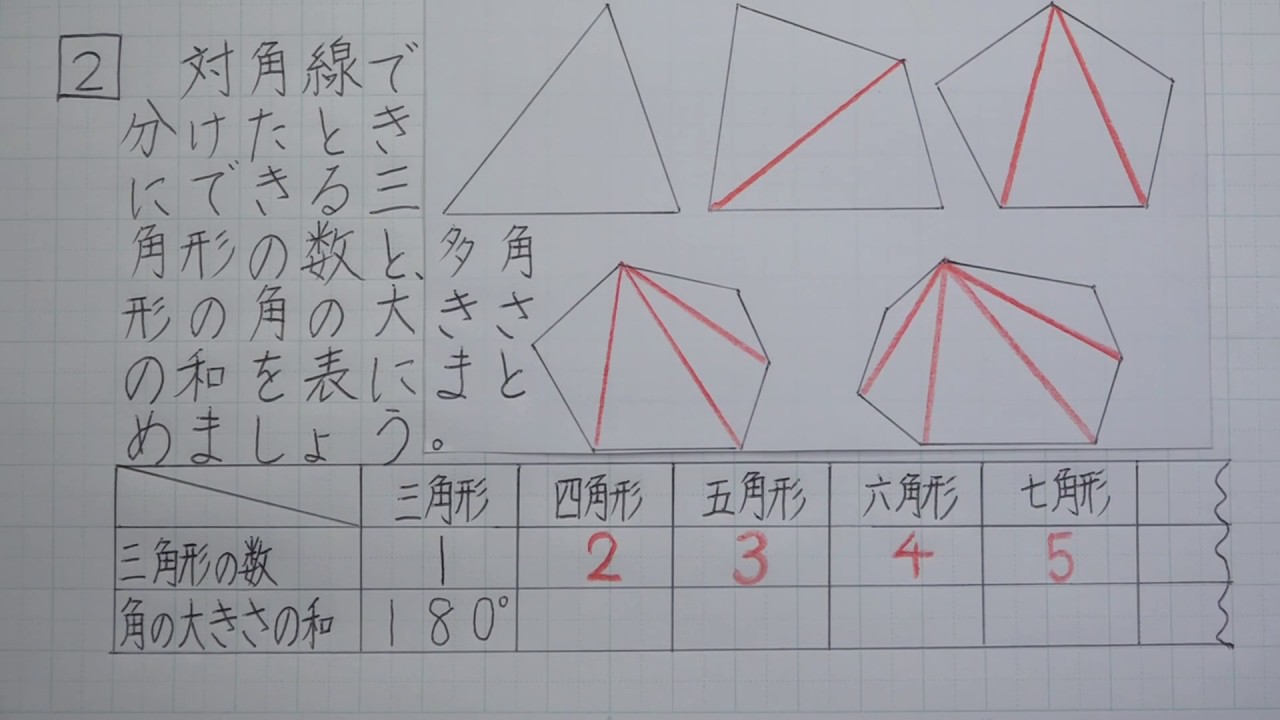
三角形の合同条件を使って、合同な三角形を見つける方法! 証明の書き方合同な三角形の証明問題の書き方を基礎から解説! 直角三角形証明問題の書き方とは?合同条件の使い方を徹底解説! 二等辺三角形の角度の求め方 厳選6問解説!直線図形 (入試問題) → 携帯版は別頁 == 直線図形と角 == (入試問題) 要点 (1) 三角形の内角の和は180°に等しい. (2) 三角形の外角は,それと隣り合わない2つの内角の和に等しい. ≪例≫ (1) 上の図において ∠A∠B∠C=180° (2) 上の図において ∠ACD 第169問 角度の和 図形ドリル 5年生 6年生 正五角形 正六角形 正方形 角度の和 ★★★☆☆☆ (中学入試標準レベル) 思わず「お~~! ! 」と言いそうな良問を。 受験算数の定番からマニアックな問題まで。

五角形 Wikipedia
五角形の角度
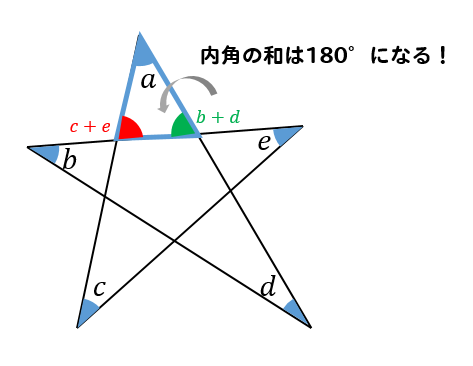
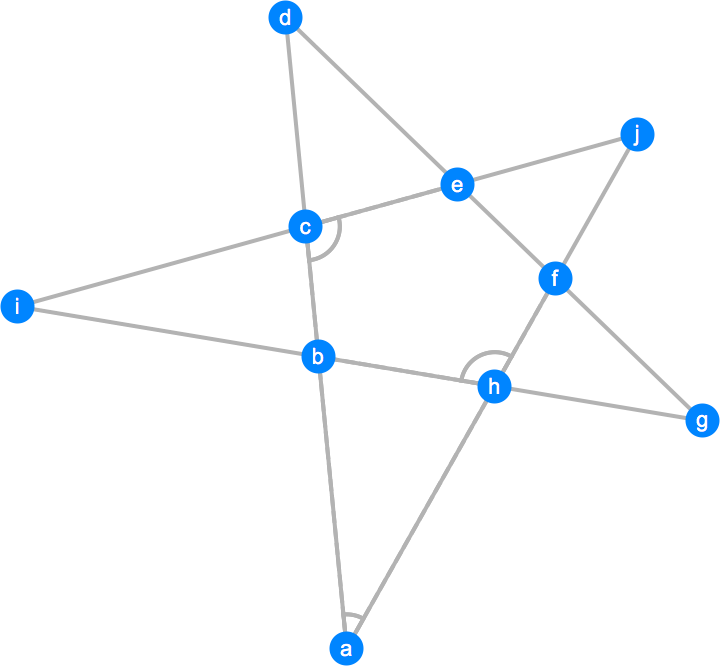
五角形の角度-1) 頂角の和が180度になる星形多角形を調べよう。 2) 星形偶数多角形の性質を調べよう。 ・星形五角形の頂角の和を求めるときに使った, の考え方がよく使われていることに気づいた生徒は数人。 <生徒のレポート例> 正五角形に付随する角度と黄金比の関係 前回の記事『 正角錐の二面角の公式 』では、「初等幾何と2次方程式を駆使して、正五角形にまつわる諸量が黄金比 と関連付けられる事」について触れないで話を進める予定だったがそもそも星形大正十二面体まで話が及ばなかったので取り消し線を
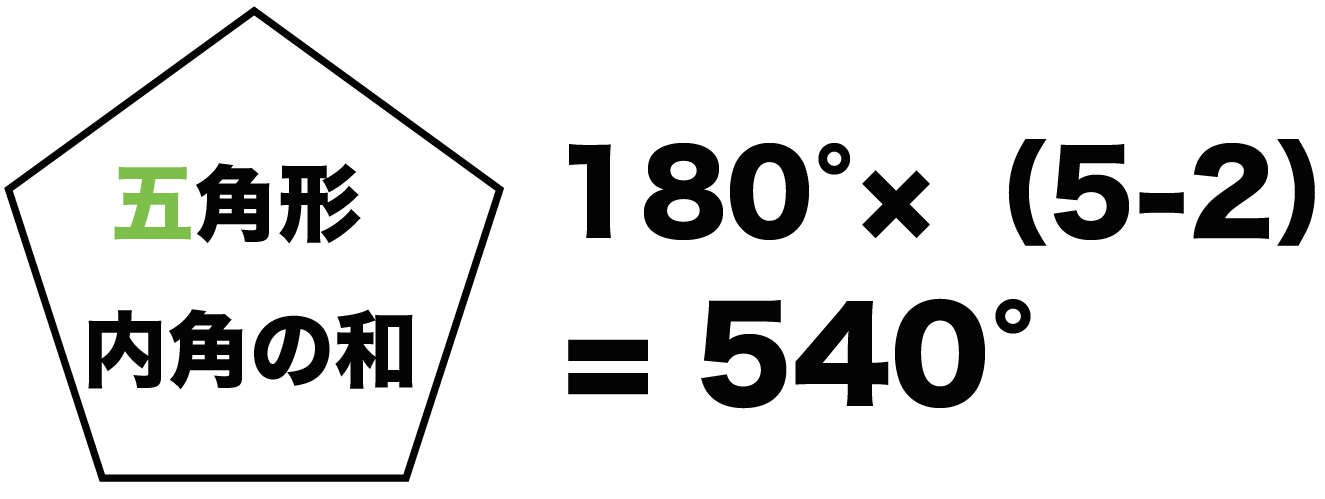



簡単公式 五角形の内角の和を3秒で計算できる方法 Qikeru 学びを楽しくわかりやすく
5/8/13 90-36 で、54° これなら 暗算でできそうですね。 正五角形の内角は、この底角2つ分ですから 54×2 で 108° このように 36°と54° 、そしてそれらの2倍の72°と108° が正五角形折った角度(渋谷教育学園渋谷中学 12年) 角度と長さと面積(フェリス女学院中学 09年) 重なった正六角形と正五角形(奈良学園登美ヶ丘中学 09年、早稲田中学 10年) 直角三角形の合同条件(市川中学 10年) 角度問題の定石とは?形 なし なし なし 四 角 形 なし なし なし 五 角 形 なし なし 六 角 形 なし なし 七 角 形 なし 八 角 形 なし 九 角 形 十 角 形 活動σ規則性を見つけ、式に表す。 ※m 点とばし星型n 角形の内角の和は180°×(n-2-2m)と表すことができる。 180° 360° 540
1/5/ 問題 (奈良学園登美ヶ丘中学 09年、早稲田中学 10年 女子学院中学 14年 受験問題 算数) 難易度★★★ 1 1辺の長さが等しい正五角形と正六角形を、下の図Ⅰのように1つの辺を重ねました。このとき、アの角度は何度ですか。31/5/21 正五角形の内角は108° するとここを頂角にした二等辺三角形が見えてきたと思うので、底角を出す。さっそく二等辺三角形が出てきてうれしい。 ここの角度が36°と求まる 正方形の内角は90°なので、下の赤い角は180-(36+90)=54(°)。 ここは54°星形五角形の角度 星形五角形の角度 Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device
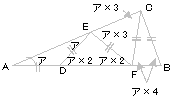
Jw_cad (JWW) ではじめてCAD作図するかたに、多角形、文字、寸法線の作図パターンの基本を説明、多様な機能を搭載した汎用2DCAD、Jw_cad (JWW)の入門の手助けとなります。星形五角形の印を つけた5つの 角の和は何度でしょう。 どんな星形五角形でも印をつけた5つの角の和は180°に なる。その理由をできるだけ多くの方法で説明してみよう。 ①ブーメラン型の図形 の角度を利用 ②補助線を引く⇒三角形 の内角の和5年 学研教育情報資料センター 算数 学習相談 小/算数/5年/図形/ 合同な図形/理解シート



6年課題 算数 の問題解説1 課題の算数プリントの中で 間違いが多かった問題の解き方を考えましょう この問題は 五角形の5つの角の和の求め方を説明する問題です まず ひろとくんの考え方をわかりやすく考えてみましょう 問題の五角形の中




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学
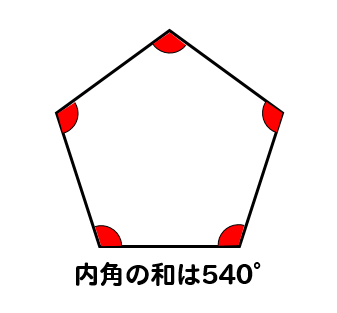
10/3/10 正四角形(正方形)は対角線で三角形2個に分けられるので 正方形の内角の和は180°×2=360° 同じように考えて 正五角形は三角形3個分で180°×3=540° 正六角形は三角形4個分で180°×4=720° 各角の大きさは 正五角形は540°÷5=108° 正六角形は720°÷6=120° 「一辺の角度は何℃か」はわかりませんでした。五角形は、安定する。 親指と人指し指を使って五面のうち三面を支持することで、歯ブラシが安定して磨くことが可能です。 ヘッドの幅が広いから、 2分間磨きでも 効率よく磨ける。 歯科医院で指導や販売されている一般の歯ブラシのほとんどが、3列Afj, bgf,等の5つの三角形の内角の和から,五角形の外角の和2つ分を引いて, 180×5-360×2 =180° 外側の五角形から付け足した三角形5つ分を引き,内側の五角形をたすと, 180×(5-2)-180×5 +180×(5-2)=180°



ペンタゴンボールの型紙 エクセルvbaで正五角形を作図してみましたpart 2 日だまりのエクセルと蝉しぐれ




数学 中2 53 角度チャレンジ Lv 1 Youtube
7/5/19 例題のような一筆書きした図形を「 星形五角形 」,「 星形七角形 」といいます。 9,11,13,などの奇数であれば,同様の星形を作れ,角度の和はすべて180°となります。 ミニカードを作10/6/ この形は外角の関係を利用して考えます。 補助線を真ん中にひくと、へこみの部分は 左側の三角形の外角右側の三角形の外角 になっていることがわかります。 星型 星の形をしている五角形です。 これは、ブーメラン型の応用で考えます。18/3/21 三角形の内角の和は180°なので、五角形の内角の和は、180°×3=540° になります。 多角形の角の性質を下の表にまとめました。 必ず覚えてください。




正五角形の長さや面積の導出 数学の偏差値を上げて合格を目指す



1
(1)九角形の内角の和は何度ですか。 (2)正五角形の1つの内角は何度ですか。 (3)1つの外角が°の正多角形は正何角形ですか。 (4)六角形の対角線の本数は何本ですか。 (5)下の図のアの角度は何度ですか。正五角形の内角の和は 180 x (52) = 540 1つの内角の角度は 540 / 5 = 10 正六角形の形は、鉛筆やサッカーボールなど、わりと身近にあふれています。 しかし実際に正六角形を書けと言われたら、書くことはできますか。 今回は、コンパスや定規などの道具を二等辺三角形 足が5本(正五角形? )の椅子を購入することを考えてます。 足の横幅で、最長の幅は記載があるが、最小の幅の記載がない。 がないため2等辺三角形の高さが最小幅と考えネットで公式はたくさん出てくるが自分で計算できなかったのでお



ペンタゴンボールの型紙 エクセルvbaで正五角形を作図してみました 日だまりのエクセルと蝉しぐれ



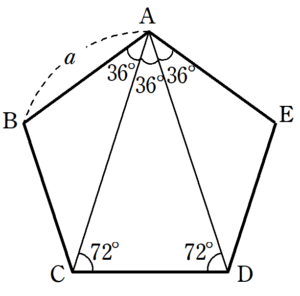
図 正五角形abcdeは正五角形で 三角形fcdは正三角形です xの角度を求め Yahoo 知恵袋
4/4/19 株式会社ベネッセコーポレーションのプログラミング教育の取り組みや、プログラミング教育に関する国内外のニュースや事例を紹介するWebページです。 小5算数 内角の大きさを求めて正多角形を作図しよう について紹介します。8/5/19 そうです。正二十面体の12個の頂点を切り取ってできた正五角形は12枚、正二十面体の元の面からできている正六角形はもちろん枚ですね! (数学科 園田毅) "A soccer ball is a famous solid!" There are many designs with soccer balls nowすべて 多角形を,正多角形といいます。 2 下の円を使って,正九角形をかきましょう。 ( 点) 3 下の図は正五角形です。 あからうの角度は何度ですか。 (30 点) あ い正五角形の性質 正三角形・正方形・正六角形に引き続き、正五角形編です。 相似 まずは角度に注目。 内角の和



平面図形の角度 第81問 正五角形 女子学院中学 入試問題 13年 平成25年度 算数 まいにち一題 中学受験過去問題研究
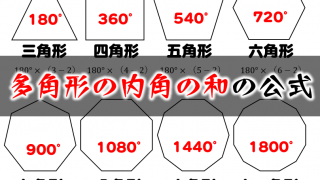



多角形 の内角の角度 計算ドリル 問題集 数学fun
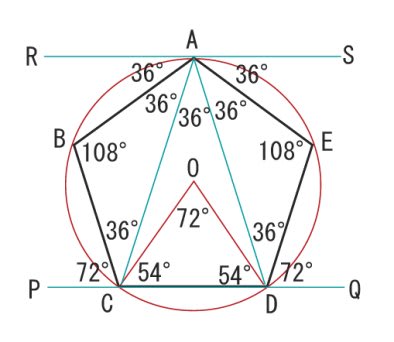



正五角形というだけで 分かる角度は 名寄 算数数学教室より



正五角形です あ い うの角度の求め方教えてください あ36 Yahoo 知恵袋
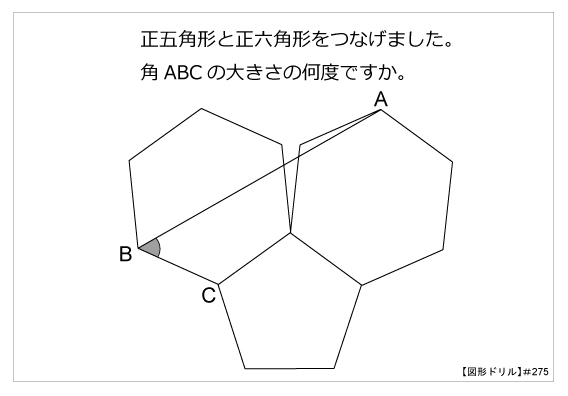



図形ドリル 第275問 正五角形と正六角形 算数星人のweb問題集 中学受験算数の問題に挑戦




多角形の内角の和の公式を3通りの方法で証明する 具体例で学ぶ数学
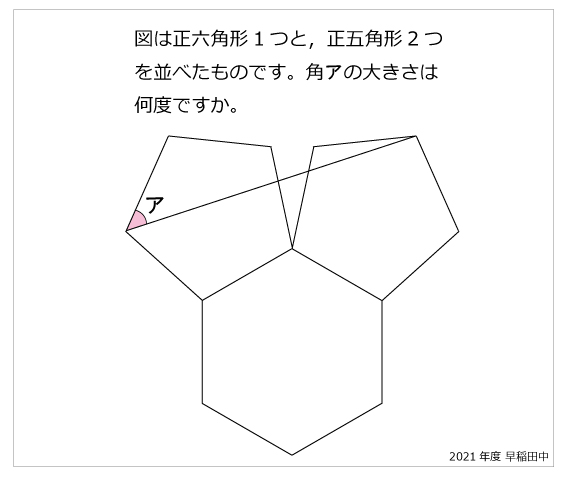



今年の1問 21年早稲田中 正五角形と正六角形 算数星人のweb問題集 中学受験算数の問題に挑戦
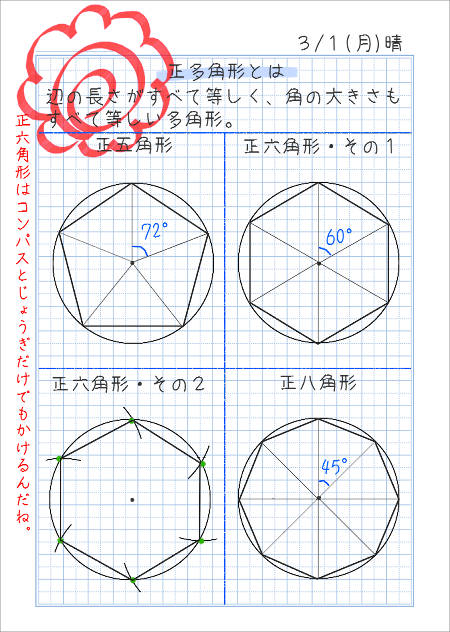



いろいろな正多角形をかいてみよう 家庭学習レシピ



正五角形というだけで 分かる角度は 名寄 算数数学教室より




五角形 Wikipedia



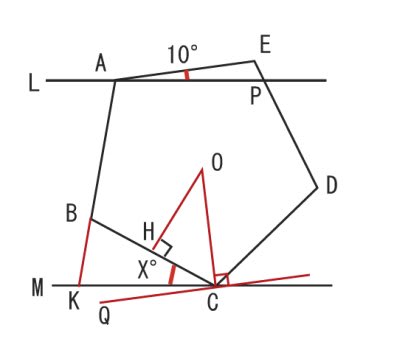
正五角形と二本の平行線があるとき Xの角度はいくつか 回答解 Yahoo 知恵袋



正多角形の内角と中心角 家紋の描き方007b 夏貸文庫



4 6 六角形と正五角形の角度を求めるには さんすうがく パート 2



1



全ての角度が等しい五角形には例えばどんな形のものがありますか Yahoo 知恵袋




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun



この方法で星型五角形の五つの内角の和の求め方をおしえてください A Yahoo 知恵袋




小学校5年 算数 正多角形の角の大きさ Youtube



正五角形折った角度 渋谷教育学園渋谷中学 12年 これが中学入試に出た図形問題



正五角形を描く ウソの国ー詩と宗教 戸田聡 St5402jp




小学5年生 正多角形 算数 Active Learning 学院



早稲田11 2 の 1 角度 正五角形と正三角形が重なった図形 気まぐれ解説カフェ 仮



折った正五角形の角度 ラ サール中学 2014年 これが中学入試に出た図形問題



平行線と角度 8 ネット塾



正多角形の面積の公式 Fukusukeの数学めも



Tableauでレーダーチャートをつくってみた 応用編 Tabろぐ



正五角形というだけで 分かる角度は 名寄 算数数学教室より



角度




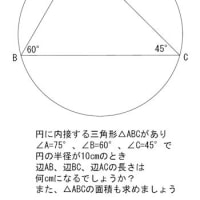
角度を求めて下さい 角度を求めて下さい 図のように 円に内接する 数学 教えて Goo



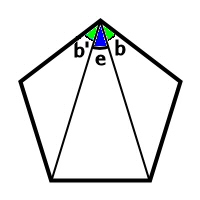
星形の角度 内角の和の求め方を問題解説 数スタ



簡単公式 五角形の内角の和を3秒で計算できる方法 Qikeru 学びを楽しくわかりやすく
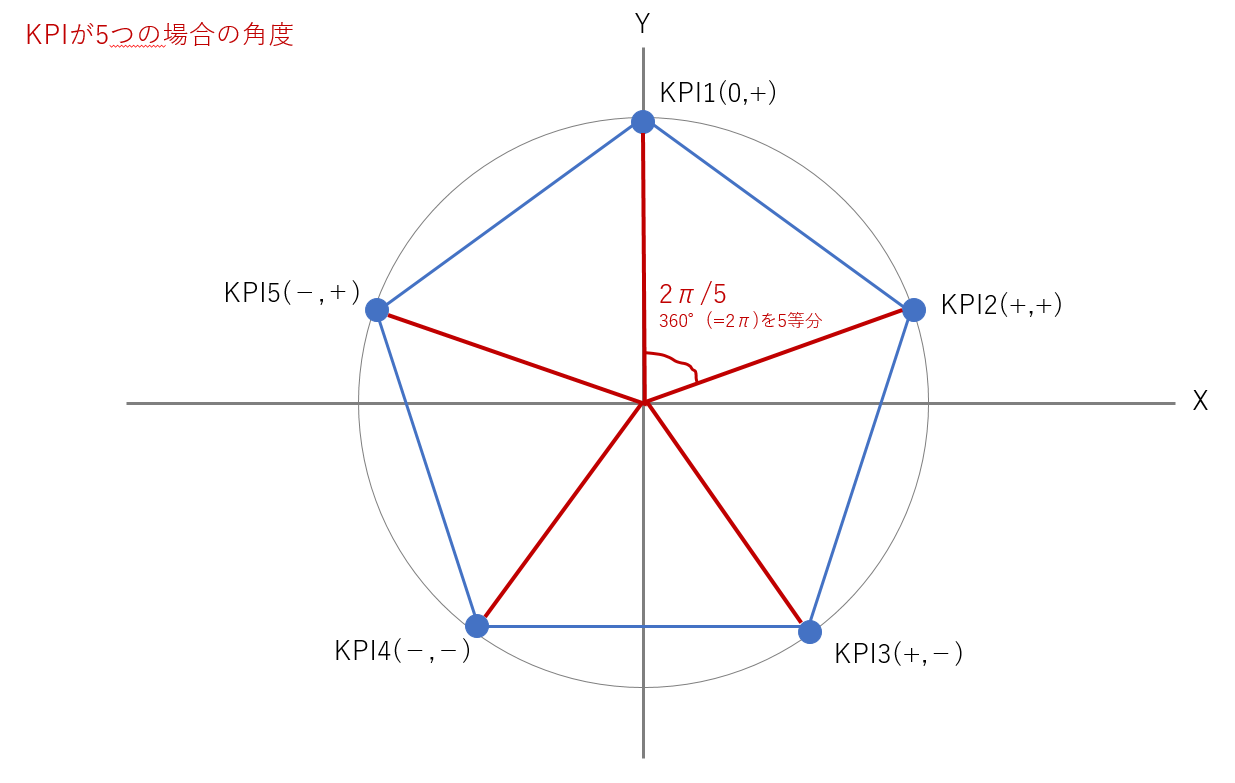



Tableauでレーダーチャートをつくってみた 応用編 Tabろぐ
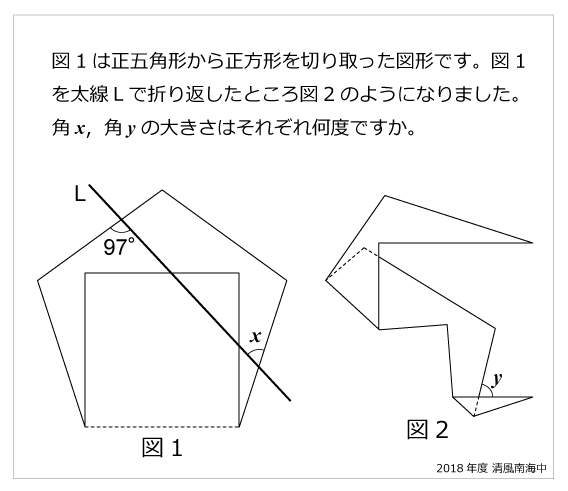



正五角形 算数星人のweb問題集 中学受験算数の問題に挑戦



1



正五角形というだけで 分かる角度は 名寄 算数数学教室より




数学 中2 51 多角形の内角と外角の和 基本編 Youtube




小5 算数 小5 54 正多角形 Youtube



ペンタゴンの秘密 正五角形の謎を解く 空間情報クラブ 株式会社インフォマティクス



正五角形 正六角形 の 内角の和 と 一辺の角度は何 か 教 Yahoo 知恵袋
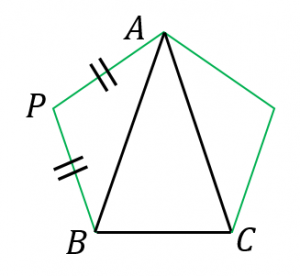



正五角形の対角線の長さと高さ 具体例で学ぶ数学



敷き詰めの探究 Part 1 数理女子



正五角形




正多角形の 内角が あっという間に分かる術 名寄 算数数学教室より




道具別 五角形の簡単な書き方 コンパス フリーハンド 学習情報ならtap Biz




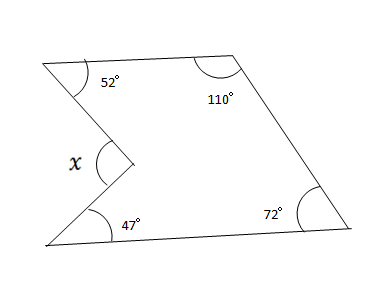
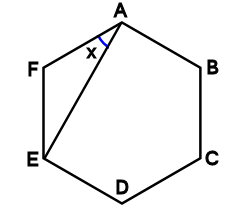
Xを求める問題です 教えてください Clear



1




多角形の内角の和の公式と外角の和を利用した角度の求め方




どこで間違えてるか教えて下さい ˊᵕˋ Xの角度を求める問題です Clear



未知の角度について解く Wolfram言語 12の新機能
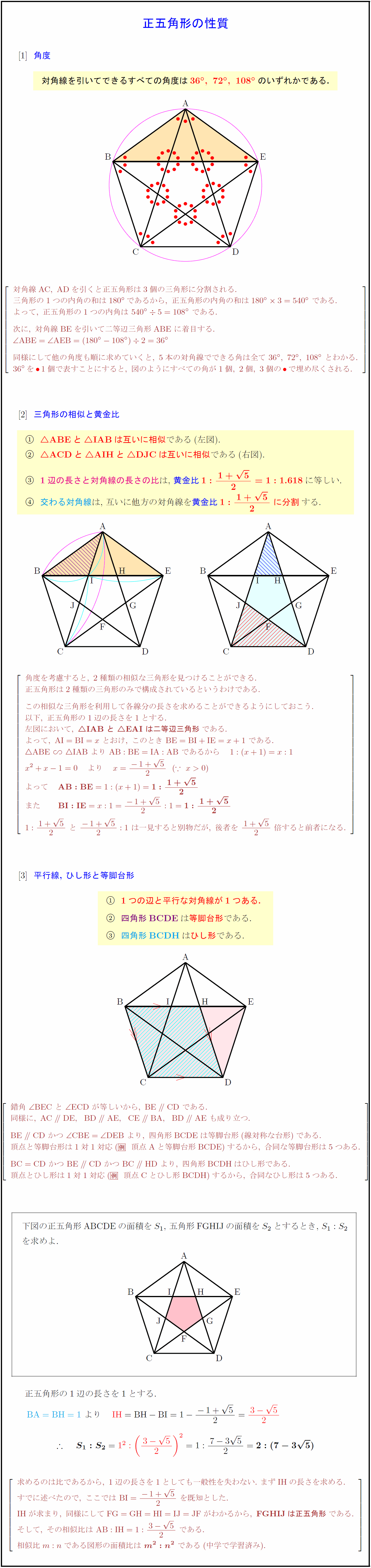



高校数学a 正五角形の性質 三角形の相似 黄金比 等脚台形 ひし形 受験の月
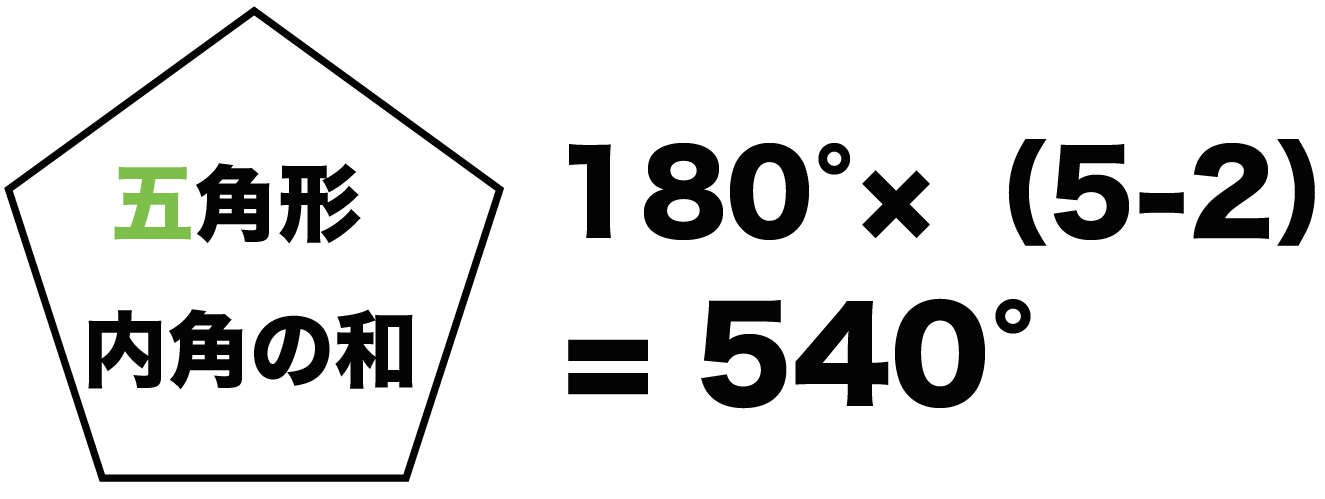



簡単公式 五角形の内角の和を3秒で計算できる方法 Qikeru 学びを楽しくわかりやすく



ペンタゴンの秘密 正五角形の謎を解く 空間情報クラブ 株式会社インフォマティクス
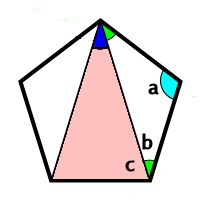



正五角形の中の角度



図形 正五角形の分解 父ちゃんが教えたるっ




180 Descubre Como Resolverlo En Qanda



Lとmは平行であり 五角形abcdeは正五角形である Xの Yahoo 知恵袋




小5 算数 小5 33 五角形 六角形 多角形 Youtube
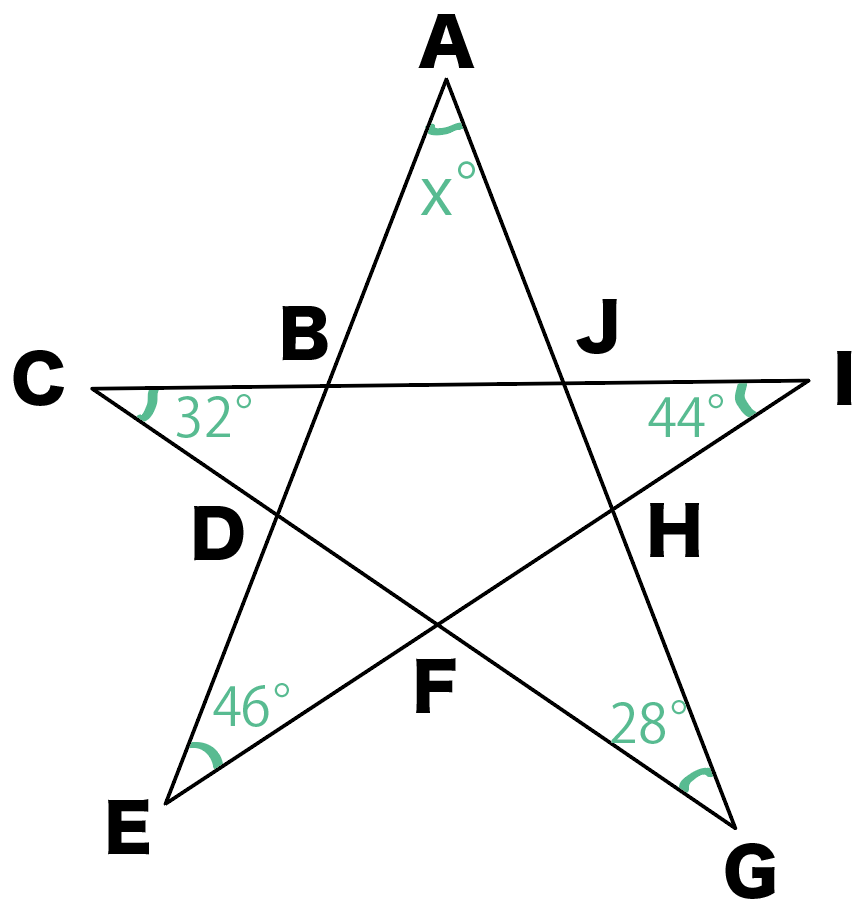



星形の角度の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




五角形 Wikipedia



角度 五角形 中学から数学だいすき




正五角形に付随する角度と黄金比の関係 萌えとかプログラミングとか




簡単公式 五角形の内角の和を3秒で計算できる方法 Qikeru 学びを楽しくわかりやすく
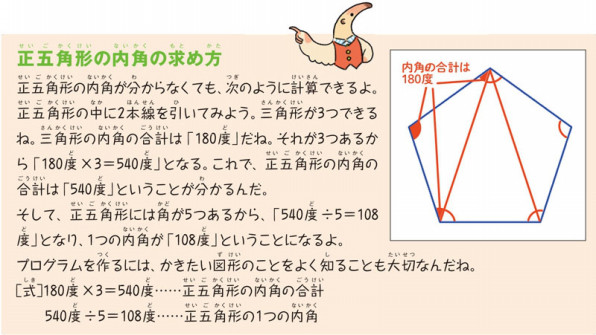



スクラッチ入門 16 正五角形をかいてみよう はじめる 楽しむ プログラミング こどもプログラミング教育のツボ ジャムハウス




多角形の内角の和 は何度なのか を説明します おかわりドリル
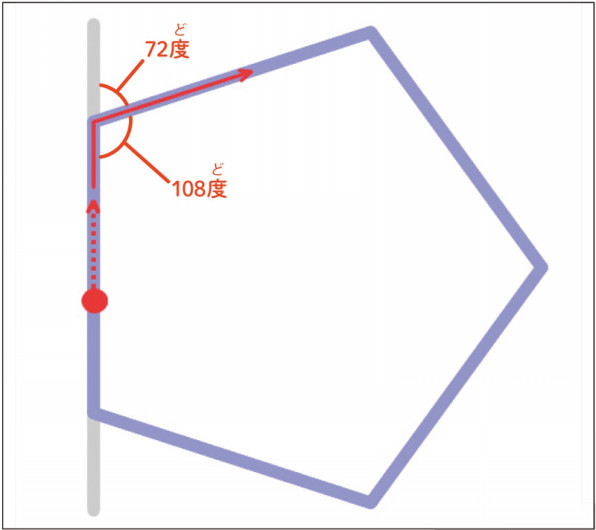



スクラッチ入門 16 正五角形をかいてみよう はじめる 楽しむ プログラミング こどもプログラミング教育のツボ ジャムハウス




簡単公式 五角形の内角の和を3秒で計算できる方法 Qikeru 学びを楽しくわかりやすく



第65問の解答
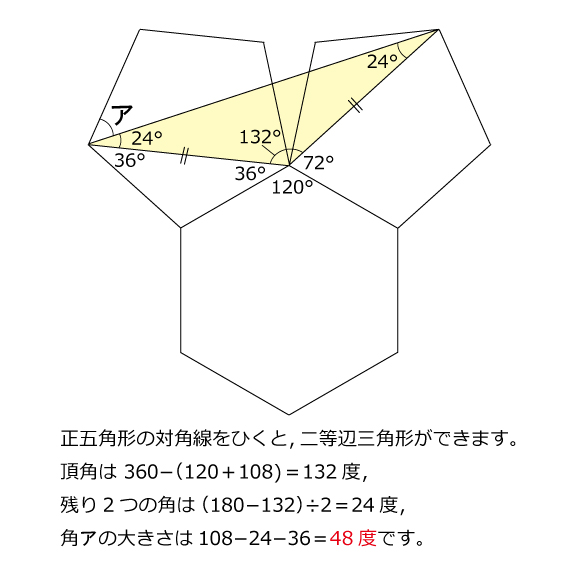



今年の1問 21年早稲田中 正五角形と正六角形 算数星人のweb問題集 中学受験算数の問題に挑戦



重なった正六角形と正五角形の角度 奈良学園登美ヶ丘中学 09年 早稲田中学 10年 算数解法の極意



正五角形の内角 外角
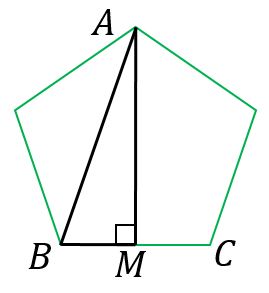



正五角形の対角線の長さと高さ 具体例で学ぶ数学



正五角形というだけで 分かる角度は 名寄 算数数学教室より



旧バージョン 5年算数 図形の角と合同 8 多角形の角の大きさの和を調べよう Youtube



幾何大王からの挑戦状 角度の問題 24 解答例




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学



正五角形の中の角度



正多角形の1つの内角 外角を求める方法を問題解説 数スタ



正五角形の中の角度
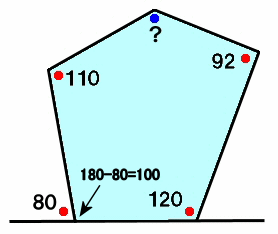



五角形の内角



角度 五角形 中学から数学だいすき
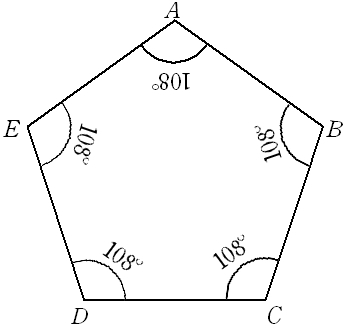



茗渓予備校 科目別データベース



大妻11 7 角度 五角形と二等辺三角形が組み合わさった問題 気まぐれ解説カフェ 仮




多角形の内角の和 算数の公式覚えてますか
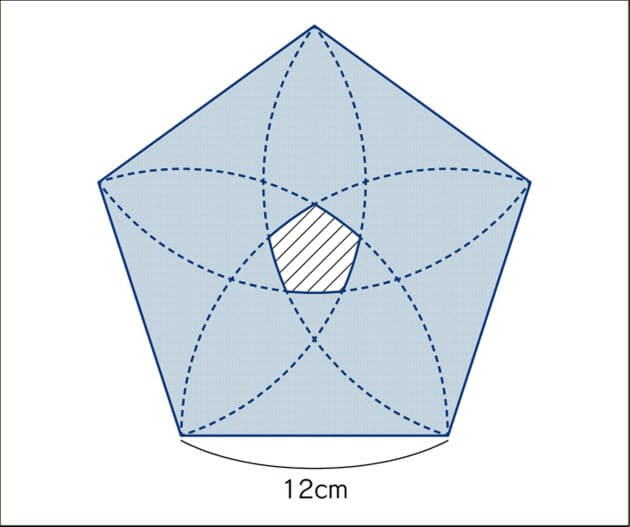



算数オリンピックに挑戦 第23回 Nikkei Style
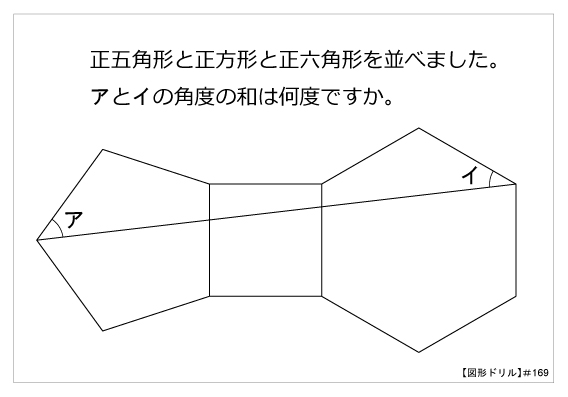



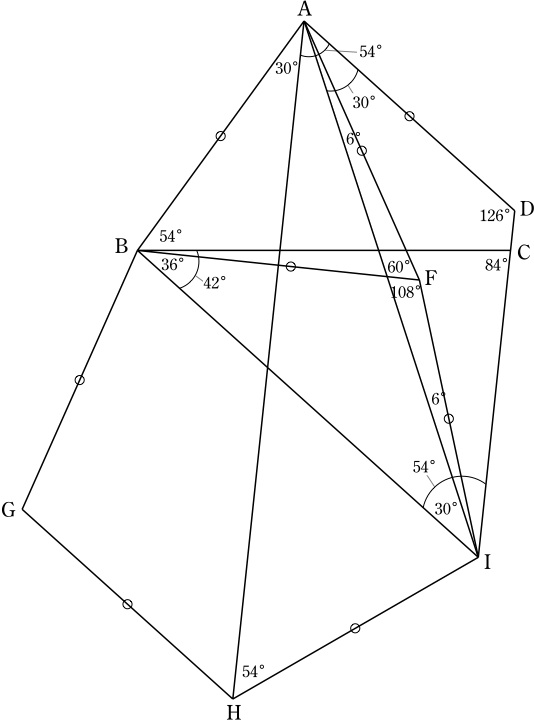
図形ドリル 第169問 角度の和 算数星人のweb問題集 中学受験算数の問題に挑戦



角度 五角形 中学から数学だいすき



Xの角度を教えてください円の中は正五角形です 正五角形の各頂 Yahoo 知恵袋




星の五角形の問題です どうやって角度を求めればいいですか Clear




課題学習の指導 数学



多角形の内角と外角 思考力を鍛える数学




五角形と星形の相関図 Scratch Pythonプログラミング 作例




五角形 Wikipedia




発展 円に内接する正五角形の作図 デザインあ おとなスペシャルで紹介されてたやつ なかけんの数学ノート



正五角形と正六角形の角度 女子学院中学 14年 どう解く 中学受験算数




この考え方を教えて欲しいです Clear




多角形の内角の和 外角の和の公式 数学fun



0 件のコメント:
コメントを投稿